www.industrieweb.fr
22
'08
Written on Modified on
Les ingénieurs financiers de Mitsubishi UFJ Securities International font appel à Maple pour le développement de produits « multi-asset »
La toute dernière version de Maple™ 12, produit phare de Maplesoft™, propose aux professionnels de la finance quantitative une plateforme d’optimisation de leur productivité et de leur efficacité. Le puissant moteur de calcul mathématique et les algorithmes sophistiqués de Maple créent un environnement de modélisation des produits financiers et d’optimisation des processus extrêmement avancé.
« Lorsque les professionnels de la modélisation ou de la conception, et les chercheurs dans toutes les disciplines décident d’utiliser Maple pour réaliser leurs travaux de recherche fondamentale ou pour développer leurs applications industrielles, ils ont en fait les mêmes objectifs que les professionnels de la modélisation financière » avance Igor Hlivka, coprésident du groupe d’analyse quantitative « Quantitative Analytics Group » chez Mitsubishi UFJ Securities International à Londres et utilisateur de longue date de Maple pour des application financières. « Les utilisateurs souhaitent disposer d’une plate-forme robuste pour la conception, le calcul, le contrôle ex post et la visualisation de leurs tâches d’élaboration de produits. »
Le principal avantage de Maple est lié à ses outils analytiques très utiles pour la modélisation des produits financiers. Rien n’est, en effet, plus précieux aux yeux d’un ingénieur financier que la vitesse de calcul et la facilité de mise en œuvre qui caractérise les solutions symboliques pour la modélisation des produits. « Dans le monde des options financières, qui constituent, à n’en pas douter, le poste le plus avancé du monde de la finance, il n’est pas toujours facile d’obtenir des résultats analytiques, et les calculs à mettre en œuvre en ce sens peuvent être longs et fastidieux. C’est ici que Maple simplifie grandement les choses. En effet, si une solution symbolique existe, Maple l’identifie rapidement et avec précision » souligne Igor Hlivka.
Ce même Igor Hlivka vient de mettre au point une série d’applications utilisant Maple pour le développement de produits « multi-asset » (actifs diversifiés) et l’élaboration de solutions semi-analytiques en réponse à des options non standard dans les cas où les processus stochastiques multivariés jouent un rôle déterminant.
Application traitant des options avec ajustement des taux de change
Les options de change ajustées permettent aux investisseurs d’échanger des options sur des actifs étrangers sans s’exposer au risque de change. Ces options introduisent néanmoins des facteurs stochastiques supplémentaires qui transforment l’espace univarié traditionnel en un espace bivarié ou multivarié.
Cette application modélise les différentes méthodes utilisées par les praticiens des marchés pour ajuster les instruments financiers et les évaluations des options lorsque les gains sont convertis en différentes devises. Cela démontre que changer la mesure de la probabilité contribue de manière importante à l’identification de solutions.
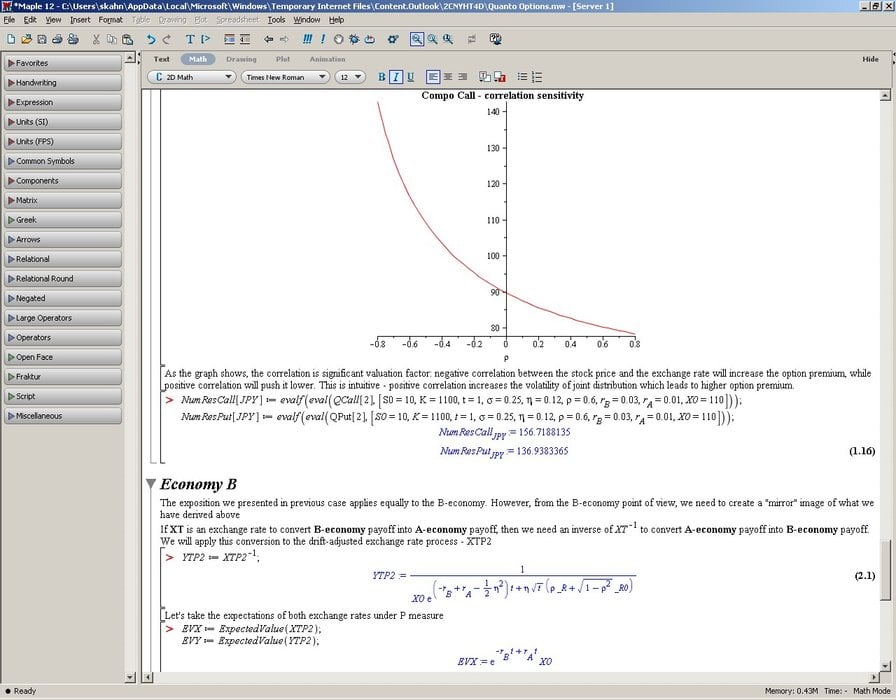
Les fonctions statistiques de Maple sont un outil essentiel permettant de modéliser la volatilité des équations différentielles de la stochastique dominante et des taux de change, mais aussi des valeurs probables. En outre, les outils de visualisation de Maple permettent de démontrer que l’existence d’une relation négative entre le niveau du cours et le taux de change (ce qui renforce la volatilité) augmente la prime alors qu'une relation positive aura pour effet de la réduire.
Application concernant les options asiatiques
Contrairement à ce qui se passe avec les contrats d’option traditionnels, les professionnels de la finance peuvent, ici, se baser sur la valeur moyenne de l’actif sous-jacent pendant la durée totale du contrat et non pas sur sa valeur finale. Ces contrats, appelés options asiatiques, constituent un outil plus attractif pour les trésoriers d’entreprise et les gestionnaires de risques qui créent des programmes de couverture. Les moyennes géométriques continues débouchent sur des solutions fermées destinées aux options asiatiques, ce qui constitue la vocation première de cette application. Si l’application développée par Igor Hlivka concerne les niveaux des cours, elle permet néanmoins d’évaluer très facilement les dynamiques log-normales.
Les outils de différentiation symbolique de Maple servent notamment à générer une expression fermée de la sensibilité des options asiatiques à la variation du niveau du cours sous-jacent. L’expression qui en résulte indique que la sensibilité est la plus forte lorsque le prix du titre est proche du prix d’exercice, et qu’elle présente le plus grand risque de variation lorsque la volatilité tombe à zéro.
Application d’options perpétuelles
Contrairement aux options standard, les options perpétuelles ne présentent ni échéance déterminée ni limites d’exercice. Cette application utilise Maple afin de résoudre les équations différentielles ordinaires en vue de leur évaluation. Elle fournit, en outre, une solution fermée concernant le niveau du cours qui constitue une optimisation de la valeur d’un stellage perpétuel. Pour ce faire, elle effectue la différentiation des formules en fonction de leur valeur, en les définissant d’abord comme égales à zéro, puis par une résolution du niveau du cours.
« J’ai utilisé plusieurs fois Maple sur des processus univariés, mais je n’avais jamais testé son interface multivariée. Cette tâche s’est avérée à la fois ambitieuse et gratifiante, » ajoute Igor Hlivka. « J’ai eu, une fois de plus, l’occasion de constater que Maple était parfaitement capable de traiter ce genre de routines. En appliquant diverses techniques portant sur l’évolution de la mesure de la probabilité, j’ai réussi à produire, grâce à Maple, une solution nette et théoriquement viable permettant de présenter et de visualiser de manière cohérente la séquence des différentes phases nécessaires, depuis la proposition du modèle jusqu’au résultat final. »
Les multidépendances ont tendance à être complexes et difficiles à modéliser, mais Maple simplifie cette tâche et permet de créer des outils de prévision pratiques. Grâce à Maple, les ingénieurs financiers peuvent maîtriser tous ces enjeux ; la solution produite est rapide, précise et intuitive, et elle est facilement visualisable à des fins de contrôle ex post et d’analyse de scénario. Les applications récemment créées par Igor Hlivka confirment la solide réputation des produits que Maplesoft propose aux ingénieurs financiers souhaitant disposer de solutions à la fois rapides, précises et faciles à déployer afin de répondre à tous leurs besoins de modélisation de produits au quotidien.
Le principal avantage de Maple est lié à ses outils analytiques très utiles pour la modélisation des produits financiers. Rien n’est, en effet, plus précieux aux yeux d’un ingénieur financier que la vitesse de calcul et la facilité de mise en œuvre qui caractérise les solutions symboliques pour la modélisation des produits. « Dans le monde des options financières, qui constituent, à n’en pas douter, le poste le plus avancé du monde de la finance, il n’est pas toujours facile d’obtenir des résultats analytiques, et les calculs à mettre en œuvre en ce sens peuvent être longs et fastidieux. C’est ici que Maple simplifie grandement les choses. En effet, si une solution symbolique existe, Maple l’identifie rapidement et avec précision » souligne Igor Hlivka.
Ce même Igor Hlivka vient de mettre au point une série d’applications utilisant Maple pour le développement de produits « multi-asset » (actifs diversifiés) et l’élaboration de solutions semi-analytiques en réponse à des options non standard dans les cas où les processus stochastiques multivariés jouent un rôle déterminant.
Application traitant des options avec ajustement des taux de change
Les options de change ajustées permettent aux investisseurs d’échanger des options sur des actifs étrangers sans s’exposer au risque de change. Ces options introduisent néanmoins des facteurs stochastiques supplémentaires qui transforment l’espace univarié traditionnel en un espace bivarié ou multivarié.
Cette application modélise les différentes méthodes utilisées par les praticiens des marchés pour ajuster les instruments financiers et les évaluations des options lorsque les gains sont convertis en différentes devises. Cela démontre que changer la mesure de la probabilité contribue de manière importante à l’identification de solutions.
Les fonctions statistiques de Maple sont un outil essentiel permettant de modéliser la volatilité des équations différentielles de la stochastique dominante et des taux de change, mais aussi des valeurs probables. En outre, les outils de visualisation de Maple permettent de démontrer que l’existence d’une relation négative entre le niveau du cours et le taux de change (ce qui renforce la volatilité) augmente la prime alors qu'une relation positive aura pour effet de la réduire.
Application concernant les options asiatiques
Contrairement à ce qui se passe avec les contrats d’option traditionnels, les professionnels de la finance peuvent, ici, se baser sur la valeur moyenne de l’actif sous-jacent pendant la durée totale du contrat et non pas sur sa valeur finale. Ces contrats, appelés options asiatiques, constituent un outil plus attractif pour les trésoriers d’entreprise et les gestionnaires de risques qui créent des programmes de couverture. Les moyennes géométriques continues débouchent sur des solutions fermées destinées aux options asiatiques, ce qui constitue la vocation première de cette application. Si l’application développée par Igor Hlivka concerne les niveaux des cours, elle permet néanmoins d’évaluer très facilement les dynamiques log-normales.
Les outils de différentiation symbolique de Maple servent notamment à générer une expression fermée de la sensibilité des options asiatiques à la variation du niveau du cours sous-jacent. L’expression qui en résulte indique que la sensibilité est la plus forte lorsque le prix du titre est proche du prix d’exercice, et qu’elle présente le plus grand risque de variation lorsque la volatilité tombe à zéro.
Application d’options perpétuelles
Contrairement aux options standard, les options perpétuelles ne présentent ni échéance déterminée ni limites d’exercice. Cette application utilise Maple afin de résoudre les équations différentielles ordinaires en vue de leur évaluation. Elle fournit, en outre, une solution fermée concernant le niveau du cours qui constitue une optimisation de la valeur d’un stellage perpétuel. Pour ce faire, elle effectue la différentiation des formules en fonction de leur valeur, en les définissant d’abord comme égales à zéro, puis par une résolution du niveau du cours.
« J’ai utilisé plusieurs fois Maple sur des processus univariés, mais je n’avais jamais testé son interface multivariée. Cette tâche s’est avérée à la fois ambitieuse et gratifiante, » ajoute Igor Hlivka. « J’ai eu, une fois de plus, l’occasion de constater que Maple était parfaitement capable de traiter ce genre de routines. En appliquant diverses techniques portant sur l’évolution de la mesure de la probabilité, j’ai réussi à produire, grâce à Maple, une solution nette et théoriquement viable permettant de présenter et de visualiser de manière cohérente la séquence des différentes phases nécessaires, depuis la proposition du modèle jusqu’au résultat final. »
Les multidépendances ont tendance à être complexes et difficiles à modéliser, mais Maple simplifie cette tâche et permet de créer des outils de prévision pratiques. Grâce à Maple, les ingénieurs financiers peuvent maîtriser tous ces enjeux ; la solution produite est rapide, précise et intuitive, et elle est facilement visualisable à des fins de contrôle ex post et d’analyse de scénario. Les applications récemment créées par Igor Hlivka confirment la solide réputation des produits que Maplesoft propose aux ingénieurs financiers souhaitant disposer de solutions à la fois rapides, précises et faciles à déployer afin de répondre à tous leurs besoins de modélisation de produits au quotidien.

